ASVAB Math Knowledge Practice Test 751
Pythagorean Theorem
The Pythagorean theorem defines the relationship between the side lengths of a right triangle. The length of the hypotenuse squared (c2) is equal to the sum of the two perpendicular sides squared (a2 + b2): c2 = a2 + b2 or, solved for c, \(c = \sqrt{a + b}\)
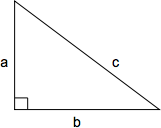
For this diagram, the Pythagorean theorem states that b2 = ?
c - a |
|
a2 - c2 |
|
c2 + a2 |
|
c2 - a2 |