Free ASVAB Practice Tests
-
Every Test is UniqueCustom software and unique templates randomize questions, answers, and variables every time you take a new test. You'll never take the same test twice!
-
1,557 Questions, Problems & Flash CardsHuge database of 668 multiple-choice questions, 135 math and algebra problems, and 754 flash cards to help you prepare for the ASVAB.
-
Detailed SolutionsGet a question wrong? All questions and problems have detailed answer explanations so you can learn exactly how to get it right the next time.
-
Know You're ReadyWant to know how you stack up? When you're done with a practice test you can compare your score to everyone else who has ever answered those questions.
-
Interactive Study GuideDetailed ASVAB study guide, MOS study guides, and line score study guides outline exactly what you should know to earn your target scores and customized tests and flash cards for each topic let you laser focus your limited study time.
-
Brand New for 2019ASVAB Test Bank has been completely redesigned for 2019 with all new questions, problems, and flash cards. And the redesign isn't done! Coming soon:
- More Content
- More questions, problems and flash cards
- Bookmarks
- Create a custom study guide with just the topics you're studying
- Score Estimator
- Custom estimate of your potential ASVAB score
Plus printable tests, Q&A, and an ad-free upgrade. Have a suggestion? Please let us know what you want!
Take an ASVAB Practice Test
Sample Practice Test Questions
Which of the following is not a prime number?
9
A prime number is an integer greater than 1 that has no factors other than 1 and itself. Examples of prime numbers include 2, 3, 5, 7, and 11.
Tension is a force that does which of the following?
stretches an object
Tension is a force that stretches or elongates something. When a cable or rope is used to pull an object, for example, it stretches internally as it accepts the weight that it's moving. Although tension is often treated as applying equally to all parts of a material, it's greater at the places where the material is under the most stress.
\({b + c \over a} = {b \over a} + {c \over a}\) defines which of the following?
distributive property for division
The distributive property for division helps in solving expressions like \({b + c \over a}\). It specifies that the result of dividing a fraction with multiple terms in the numerator and one term in the denominator can be obtained by dividing each term individually and then totaling the results: \({b + c \over a} = {b \over a} + {c \over a}\). For example, \({a^3 + 6a^2 \over a^2} = {a^3 \over a^2} + {6a^2 \over a^2} = a + 6\).
What cylinder arrangement would be most common in a four cylinder front-wheel drive vehicle?
inline
Cylinder number and arrangement depends on the purpose of the engine. Smaller (four and six cylinder) engines in front-wheel drive vehicles often use an inline design which orients cylinders vertically over the crankshaft and aligns them in a row. Other common orientations are a horizontal/opposed design which places cylinders flat facing each other with the crankshaft between them and a V-type design common in six and eight cylinder engines that features one cylinder head per block of cylinders oriented at a 60 to 90 degree angle to each other with the crankshaft at the bottom of the V.
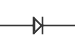
This circuit component symbol represents a(n):
diode
A diode allows current to pass easily in one direction and blocks current in the other direction. Diodes are commonly used for rectification which is the conversion of alternating current (AC) into direct current (DC). Because a diode only allows current flow in one direction, it will pass either the upper or lower half of AC waves (half-wave rectification) creating pulsating DC. Multiple diodes can be connected together to utilize both halves of the AC signal in full-wave rectification.
What is -z2 + 5z2?
To add or subtract terms with exponents, both the base and the exponent must be the same. In this case they are so add the coefficients and retain the base and exponent:
-1z2 + 5z2
(-1 + 5)z2
4z2
What part of the brain is responsible for the major senses (thinking, hearing, seeing)?
cerebrum
The cerebrum is the major part of the brain and is responsible for the main senses (thinking, hearing, seeing).
Which of the following is not an integer?
\({1 \over 2}\)
An integer is any whole number, including zero. An integer can be either positive or negative. Examples include -77, -1, 0, 55, 119.
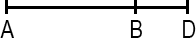
If AD = 29 and BD = 22, AB = ?
The entire length of this line is represented by AD which is AB + BD:
AD = AB + BD
Solving for AB:AB = AD - BDAB = 29 - 22
AB = 7
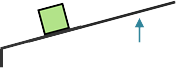 If the green box weighs 25 lbs. and 75 lbs. of force is applied 5 ft. from the fulcrum at the blue arrow, how far from the fulcrum would the green box need to be placed to balance the lever?
If the green box weighs 25 lbs. and 75 lbs. of force is applied 5 ft. from the fulcrum at the blue arrow, how far from the fulcrum would the green box need to be placed to balance the lever?
To balance this lever the torques at the green box and the blue arrow must be equal. Torque is weight x distance from the fulcrum so the equation for equilibrium is:
Rada = Rbdb
where a represents the green box and b the blue arrow, R is resistance (weight/force) and d is the distance from the fulcrum.Solving for da, our missing value, and plugging in our variables yields:
da = \( \frac{R_bd_b}{R_a} \) = \( \frac{75 lbs. \times 5 ft.}{25 lbs.} \) = \( \frac{375 ft⋅lb}{25 lbs.} \) = 15 ft.